Advertisements
Advertisements
Question
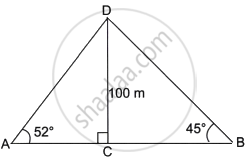
The angle of elevation of the top of a 100 m high tree from two points A and B on the opposite side of the tree are 52° and 45° respectively. Find the distance AB, to the nearest metre.
Solution
In ΔADC,
tan 52° = `"DC"/"AC" = 100/"AC"`
`\implies` 1.2799 = `100/"AC"` ...(From table)
`\implies` AC = `100/1.2799`
`\implies` AC = 78.13 m
In ΔBCD,
tan 45° = `"CD"/"BC"`
`\implies` 1 = `100/"BC"`
BC = 100 m
∴ AB = AC + BC
= 78.13 + 100
= 178.13 m
Hence, the distance AB is 178 m ...(approx)
APPEARS IN
RELATED QUESTIONS
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
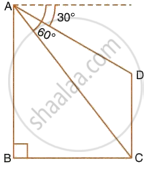
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
From a lighthouse, the angles of depression of two ships on opposite sides of the lighthouse were observed to be 30° and 45°. If the height of the lighthouse is 90 metres and the line joining the two ships passes through the foot of the lighthouse, find the distance between the two ships, correct to two decimal places.
