Advertisements
Advertisements
Question
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
Solution
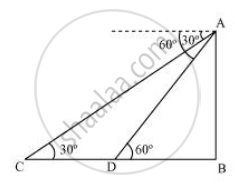
Let AB be the tower.
Initial position of ship is C , which changes to D after 3 minutes.
In ΔADB
`"AB"/"DB" = tan60^circ`
`"AB"/"DB" = sqrt(3)`
`"DB" = "AB"/sqrt(3)`
In ΔABC
`"AB"/"BC" = tan30^circ`
`"AB"/"BD + DC" = 1/sqrt(3)`
`"AB"sqrt(3) = "BD + DC"`
`"AB"sqrt(3) = "AB"/sqrt(3) + "DC"`
`"DC" = "AB"sqrt(3) - "AB"/sqrt(3) = "AB"(sqrt(3) - 1/sqrt(3))`
= `"2AB"/sqrt(3)`
Time taken by car to travel DC distance `("i.e". "2AB"/sqrt(3))` = 3 minutes
Time taken by car to travel DB distance `("i.e". "AB"/sqrt(3))`
= `3/((2AB)/sqrt(3)) xx "AB"/sqrt(3) = 3/2` = 1 min 30 secs
Thus , the total time taken is 3 minutes + 1 minute 30 seconds = 4 minutes 30 seconds.
APPEARS IN
RELATED QUESTIONS
An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
Two climbers are at points A and B on a vertical cliff face. To an observer C, 40 m from the foot of the cliff, on the level ground, A is at an elevation of 48° and B of 57°. What is the distance between the climbers?
A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28° and the angle of depression of the bottom of the pole is 13°. Calculate the height of the pole.
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
If the angle of elevation of a cloud from a point h m above a lake is α, and the angle of depression of its reflection in the lake be β, prove that distance of the cloud from the point of observation is `("2h"secα)/(tanα - tanβ)`.
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
