Advertisements
Advertisements
Question
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
Solution
Shadow of the tower = 45 m and angle of elevation = 30°
i. Let AB be the tower and BC is its shadow.
∴ CB = 45 m.
Now in right ΔABC,
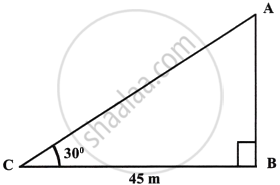
`tan theta = (AB)/(BC)`
`\implies tan 30^circ = (AB)/45`
`\implies 1/sqrt(3) = (AB)/45`
`\implies AB = 45/sqrt(3)m`.
∴ `AB = (45 xx sqrt(3))/(sqrt(3) xx sqrt(3))`
= `(45sqrt(3))/3`
= `15sqrt(3) m`.
= 15 (1.732)
= 25.980
= 25.98 m
ii. In second case,
a. Angle of elevation = 45°
And height of tower = 25.98 m
or `15sqrt(3) m`
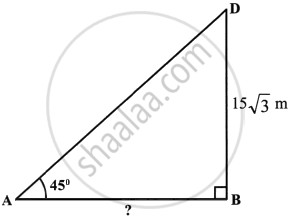
`tan 45^circ = (AB)/(DB)`
`\implies (AB)/(DB) = 1`
∴ DB = AB = 25.98 m.
b. Angle of elevation = 60°
And height of tower = 25.98 m
or `15sqrt(3) m`.
Let shadow of the tower DB = x m
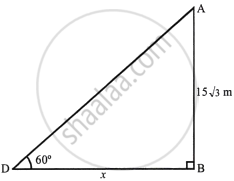
∴ `tan 60^circ = (AB)/(DB)`
`\implies sqrt(3) = (15sqrt(3))/(DB)`
`\implies DB = (15sqrt(3))/sqrt(3) = 15 m`.
Hence length of shadow = 15 m.
APPEARS IN
RELATED QUESTIONS
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60° to 30°.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
If the angle of elevation of a cloud from a point h m above a lake is α, and the angle of depression of its reflection in the lake be β, prove that distance of the cloud from the point of observation is `("2h"secα)/(tanα - tanβ)`.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
