Advertisements
Advertisements
प्रश्न
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
उत्तर
Shadow of the tower = 45 m and angle of elevation = 30°
i. Let AB be the tower and BC is its shadow.
∴ CB = 45 m.
Now in right ΔABC,
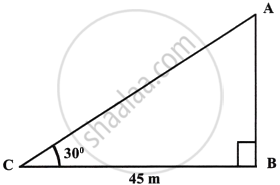
`tan theta = (AB)/(BC)`
`\implies tan 30^circ = (AB)/45`
`\implies 1/sqrt(3) = (AB)/45`
`\implies AB = 45/sqrt(3)m`.
∴ `AB = (45 xx sqrt(3))/(sqrt(3) xx sqrt(3))`
= `(45sqrt(3))/3`
= `15sqrt(3) m`.
= 15 (1.732)
= 25.980
= 25.98 m
ii. In second case,
a. Angle of elevation = 45°
And height of tower = 25.98 m
or `15sqrt(3) m`
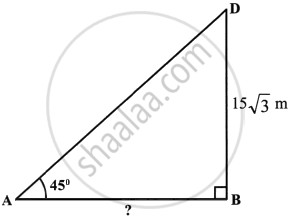
`tan 45^circ = (AB)/(DB)`
`\implies (AB)/(DB) = 1`
∴ DB = AB = 25.98 m.
b. Angle of elevation = 60°
And height of tower = 25.98 m
or `15sqrt(3) m`.
Let shadow of the tower DB = x m
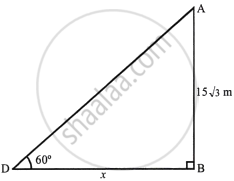
∴ `tan 60^circ = (AB)/(DB)`
`\implies sqrt(3) = (15sqrt(3))/(DB)`
`\implies DB = (15sqrt(3))/sqrt(3) = 15 m`.
Hence length of shadow = 15 m.
APPEARS IN
संबंधित प्रश्न
A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68° with the ground. Find the height, upto which the ladder reaches.
Calculate BC.
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
A man on the top of a tower observes a truck at an angle of depression ∝ where `∝ = 1/sqrt(5)` and sees that it is moving towards the base of the tower. Ten minutes later, the angle of depression of the truck is found to `β = sqrt(5)`. Assuming that the truck moves at a uniform speed, determine how much more ti me it will take to each the base of the tower?
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
The angle of elevation of the top of a 100 m high tree from two points A and B on the opposite side of the tree are 52° and 45° respectively. Find the distance AB, to the nearest metre.