Advertisements
Advertisements
प्रश्न
A man on the top of a tower observes a truck at an angle of depression ∝ where `∝ = 1/sqrt(5)` and sees that it is moving towards the base of the tower. Ten minutes later, the angle of depression of the truck is found to `β = sqrt(5)`. Assuming that the truck moves at a uniform speed, determine how much more ti me it will take to each the base of the tower?
उत्तर
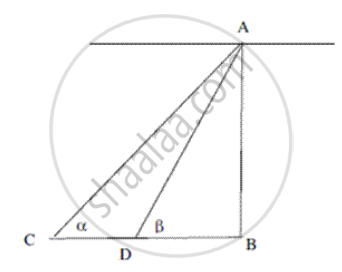
In the figure , AB is the tower . A is the position of the man. C and D are the two positions of the truck.
Let the speed of the truck be x m/sec
Distance CD = Speed × time = 600x
In right triangle ABC,
`tan α = "h"/"BC"`
It is a given that `tan α = 1/sqrt(5)`
`"BC" = "h"sqrt(5)` .. (1)
In right triangle ABD,
`tan β = "h"/"BD"`
It is given that `tan β = sqrt(5)`
`"h" = sqrt(5)"BD"`
Now , CD = BC - BD
600x = 5BD - BD
BD = 150x
Time taken = `(150"x")/"x"` = 150 seconds
Thus , the time taken by the truck to reach the tower is 150 sec = 2 min 30 sec.
APPEARS IN
संबंधित प्रश्न
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
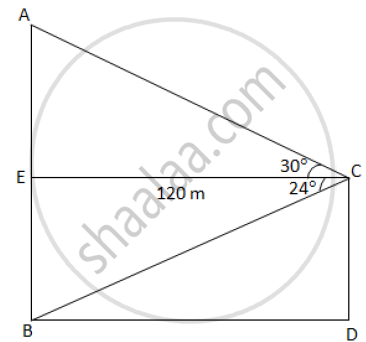
Find the height of the two towers. Give your answer correct to 3 significant figures
Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50 m.
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
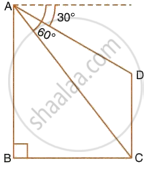
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
A vertical pole is 90m high and the length of its shadow is `90sqrt(3)`. what is the angle of elevation of the sun ?
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
