Advertisements
Advertisements
प्रश्न
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
उत्तर
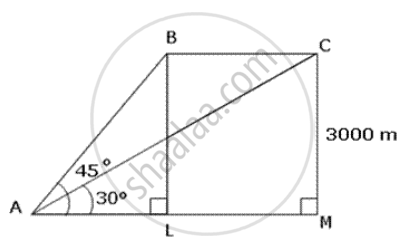
Let A be the point of observation on the ground and B and C be the two positions of aeroplane. Let BL=CM = 3000 m.
In ΔALB,
`tan 45^circ = "BL"/"AL"`
⇒ `1 = 3000/"AL"`
⇒ `"AL" = 3000`
In ΔAMC,
`tan 30^circ = "MC"/"AM"`
⇒ `1/sqrt(3) = 3000/(3000 + "LM")`
⇒ 3000`sqrt(3)` = (3000 + LM)
⇒ `"LM" = 3000(sqrt(3) - 1)`
∴ BC = `3000(sqrt(3) - 1)`
Now , time taken to travel distance BC = 15 seconds
∴ Speed of the aeroplane = `"Distance"/"Time" = (3000(sqrt(3) - 1))/15 = 200 xx 0.732 = 146.4`
Thus , the speed of the aeroplane is 146.4 m/sec
= `146.4 xx (1/1000)/(1/3600) "km/hr" = 146.4 xx 3.6 "km/hr" = 527.04` km/hr
APPEARS IN
संबंधित प्रश्न
A man in a boat rowing away from a lighthouse 150 m high, takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 45°. Find the speed of the boat.
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°; find the uniform speed of the aeroplane in km per hour.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
From a point 10 m above the ground , the angle of elevation of the top of a tower is α and the angle of depression is β . If tan α = `5/2` and tan β = `1/4` , calculate the height of the tower to the nearest metre .
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
An aeroplane is flying horizontally along a straight line at a height of 3000 m from the ground at a speed of 160 m/s. Find the time it would take for the angle of elevation of the plane as seen from a particular point on the ground to change from 60⁰ to 45⁰. Give your answer correct to the nearest second.
