Advertisements
Advertisements
Question
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
Solution
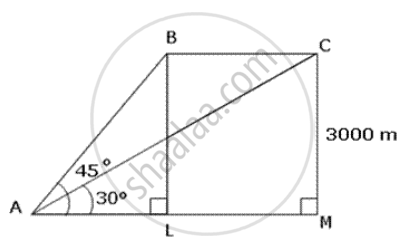
Let A be the point of observation on the ground and B and C be the two positions of aeroplane. Let BL=CM = 3000 m.
In ΔALB,
`tan 45^circ = "BL"/"AL"`
⇒ `1 = 3000/"AL"`
⇒ `"AL" = 3000`
In ΔAMC,
`tan 30^circ = "MC"/"AM"`
⇒ `1/sqrt(3) = 3000/(3000 + "LM")`
⇒ 3000`sqrt(3)` = (3000 + LM)
⇒ `"LM" = 3000(sqrt(3) - 1)`
∴ BC = `3000(sqrt(3) - 1)`
Now , time taken to travel distance BC = 15 seconds
∴ Speed of the aeroplane = `"Distance"/"Time" = (3000(sqrt(3) - 1))/15 = 200 xx 0.732 = 146.4`
Thus , the speed of the aeroplane is 146.4 m/sec
= `146.4 xx (1/1000)/(1/3600) "km/hr" = 146.4 xx 3.6 "km/hr" = 527.04` km/hr
APPEARS IN
RELATED QUESTIONS
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be 60°. Assuming that the boat sails at a uniform speed, determine:
- how much more time it will take to reach the shore?
- the speed of the boat in metre per second, if the height of the cliff is 500 m.
Find AD.

The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
If the angle of elevation of a cloud from a point h m above a lake is α, and the angle of depression of its reflection in the lake be β, prove that distance of the cloud from the point of observation is `("2h"secα)/(tanα - tanβ)`.
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
