Advertisements
Advertisements
Question
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
Solution
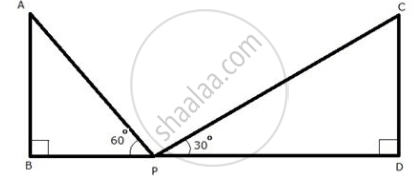
Let AB and CD be the two towers of height h m.
Let P be a point in the roadway BD such that BD = 150 m, ∠APB = 60° and ∠CPD = 30°
In ΔABP,
`(AB)/(BP) = tan 60^circ`
`=> BP = h/(tan 60^circ) = h/sqrt(3)`
In ΔCDP,
`(CD)/(DP) = tan 30^circ`
`=> PD = 1/sqrt(3)`
Now, 150 = BP + PD
`=> 150 = h/sqrt(3) + 1/sqrt(3)`
∴ `h = 150/(sqrt(3) + 1/sqrt 3)`
= `150/2.309`
= 64.95 m
Hence, height of the pillars is 64.95 m.
The point is `(BP)/sqrt(3)` from the first pillar.
That is the position of the point is `64.95/sqrt(3) m` from the first pillar.
The position of the point is 37.5 m from the first pillar.
APPEARS IN
RELATED QUESTIONS
An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
An aeroplane takes off at angle of `30^circ` with the ground . Find the height of the aeroplane above the ground when it has travelled 386m without changing direction .
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.