Advertisements
Advertisements
Question
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
Solution
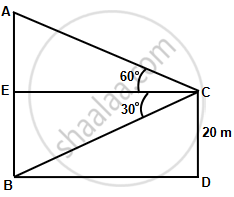
Let AB be the tower and CD be the pole.
Then ∠ACE = 60° and ∠BCE = 30°.
i. In ΔBEC,
`(BE)/(EC) = tan 30^circ`
`=> 20/(EC) = 1/sqrt(3)`
`=> EC = 20sqrt(3) m`
In ΔAEC,
`(AE)/(EC) = tan 60^circ`
`=> AE = 20sqrt(3) xx sqrt(3) = 60 m `
∴ Height of the tower = AB
= AE + EB
= (60 + 20)
= 80 m
ii. Let height of the pole be x m
∴ CD = BE = x
In ΔBEC,
`(BE)/(EC) = tan 30^circ`
`=> EC = sqrt(3)x`
In ΔAEC,
`(AE)/(EC) = tan 60^circ`
`=> (75 - x)/(EC) = sqrt(3)`
`=>` 75 – x = 3x
∴ `x = 75/4 = 18.75 m`
∴ Height of the pole is 18.75 m.
APPEARS IN
RELATED QUESTIONS
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to 30o and 60o respectively. Find:
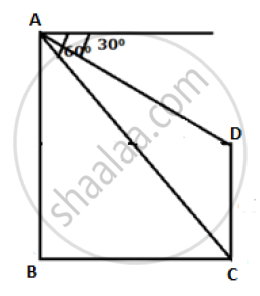
1) The horizontal distance between AB and CD.
2) The height of the lamp post.
The angle of elevation of the top of a tower, from a point on the ground and at a distance of 160 m from its foot, is found to be 60°. Find the height of the tower.
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
The horizontal distance between two trees of different heights is 100m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 150m, find the height of the first tree.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
