Advertisements
Advertisements
Question
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
Solution
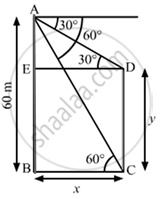
Given that AB is a building that is 60 m, high.
Let BC = DE = x and CD = BE = y
`=>` AE = AB – BE = 60 – y
i. In right ΔAED,
`tan 30^circ = (AE)/(DE)`
`=> 1/sqrt(3) = (60 - y)/(x)`
`=> x = 60sqrt(3) - ysqrt(3)` ...(1)
In right ΔABC,
`=> tan 60^circ = (AB)/(BC)`
`=> sqrt(3) = 60/x`
`=> x = 60/sqrt(3)`
`=> x = 60/sqrt(3) xx sqrt(3)/sqrt(3)`
`=> x = (60sqrt(3))/3`
`=> x = 20sqrt(3)`
`=>` x = 20 × 1.732
`=>` x = 34.64 m
Thus, the horizontal distance between AB and CD is 34.64 m.
ii. From (1), we get the height of the lamp post = CD = y
`x = 60sqrt(3) - ysqrt(3)`
`=> 20sqrt(3) = 60sqrt(3) - ysqrt(3)`
`=>` 20 = 60 – y
`=>` y = 60 – 20
`=>` y = 40 m
Thus, the height of the lamp post is 40 m.
APPEARS IN
RELATED QUESTIONS
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
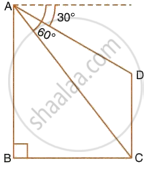
From the figure, given below, calculate the length of CD.
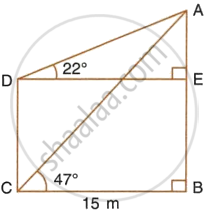
From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan `x^circ = 5/2` and the angle of depression of the foot D of the tower is y°, where tan `y^circ = 1/4`. Calculate the height CD of the tower in metres.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
The angle of elevation of a tower from a point in line with its base is `45^circ` . On moving 20m towards the tower , the angle of elevation changes to `60^circ` . Find the height of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
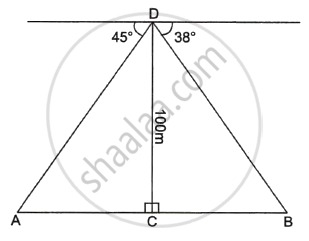
From the top of a tower 100 m high a man observes the angles of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of the tower and the ships are in the same horizontal line find the distance between the two ships A and B to the nearest metre.
(Use Mathematical Tabels for this question)