Advertisements
Advertisements
Question
From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan `x^circ = 5/2` and the angle of depression of the foot D of the tower is y°, where tan `y^circ = 1/4`. Calculate the height CD of the tower in metres.
Solution
Let CD be the height of the tower
And height of window A from the ground = 10 m
In right ΔAEC, we have
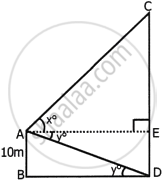
`tan x^circ = (CE)/(AE)`
`\implies 5/2 = (CE)/(AE)` ...`(∵ tan x = 5/2)`
∴ `AE = (2CE)/5` ...(i)
In right ΔAED, we have
`tan y^circ = (ED)/(AE)`
`\implies 1/4 = 10/(AE)`
∴ AE = 40
Now substituting the value AE in (i), we get
`2/5 CE = 40`
`\implies CE = (40 xx 5)/2 = 100 m`
∴ Required height of tower
CD = CE + ED
= (100 + 10) m
= 110 m
RELATED QUESTIONS
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to 30o and 60o respectively. Find:
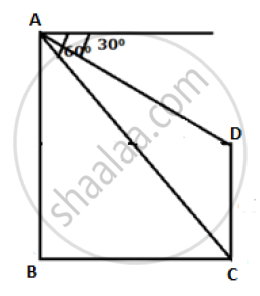
1) The horizontal distance between AB and CD.
2) The height of the lamp post.
A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28° and the angle of depression of the bottom of the pole is 13°. Calculate the height of the pole.
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.
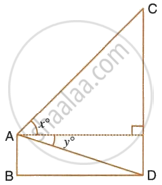
From the figure, given below, calculate the length of CD.
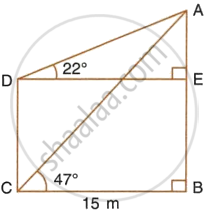
Find AD.

An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
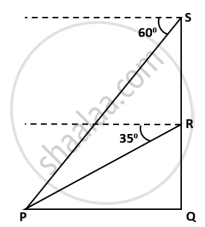
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.