Advertisements
Advertisements
Question
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
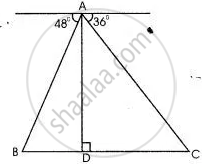
Solution
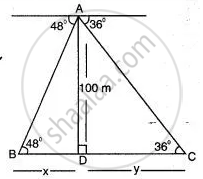
From right angle Δ ADC,
`"AD"/"CD" = tan 36°`
`100/y = tan 36°`
y = `100/tan 36°`
y = `100/(0.7265)`
y = 137.646 m
From right angle Δ ADB,
`100/x = tan 48°`
`x = 100/1.1106`
x = 90.04 m
Distance between the ships = x + y
= 137.638 + 90.04
= 227.678 m
= 228 m (appro.)
APPEARS IN
RELATED QUESTIONS
Two climbers are at points A and B on a vertical cliff face. To an observer C, 40 m from the foot of the cliff, on the level ground, A is at an elevation of 48° and B of 57°. What is the distance between the climbers?
From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if:
- the ships are on the same side of the light house,
- the ships are on the opposite sides of the light house.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
The top of a ladder reaches a pcint on the wall 5 m above the ground. If the foot of the ladder makes an angle of 30° with the ground, find the length of the ladder.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
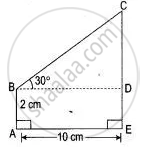
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
In figures, find the length CF.