Advertisements
Advertisements
Question
In figures, find the length CF.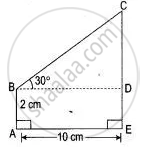
Solution
BD = AF
BD = 10 cm
In Δ BCD, we have
tan 30° = `"CD"/"BD"`
`1/sqrt3 = "CD"/10`
CD = `(10 xx sqrt3)/3` cm
CF = CD + DF = `(10 xx sqrt3)/3 + 2 cm`
= `(10 xx sqrt3 + 6)/3 cm`
APPEARS IN
RELATED QUESTIONS
Find AD.

In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
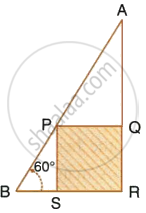
Calculate AB.

As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° from two observing points 100 m apart to his right. Find the height from which he falls and the distance of the point where he falls on the ground from the nearest observation pcint.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
