Advertisements
Advertisements
Question
A parachutist is descending vertically and makes angles of elevation of 45° and 60° from two observing points 100 m apart to his right. Find the height from which he falls and the distance of the point where he falls on the ground from the nearest observation pcint.
Solution
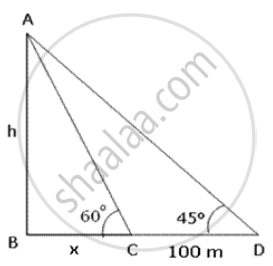
Let A be the position of the parachutist and C and D be the two observation points.
In ΔABC,
`tan 60^circ = "AB"/"BC"`
⇒ `sqrt(3) = "h"/"x"`
⇒ `"h" = sqrt(3"x")`
In ΔABD,
`tan 45^circ = "AB"/"BD"`
⇒ `1 = ("h"/("x" + 100))`
⇒ x + 100 = h
⇒ x + 100 = `sqrt(3)`x
⇒ `"x"(sqrt(3) - 1) = 100`
⇒ x = `100 xx 1/(sqrt(3) - 1) xx (sqrt(3) + 1)/(sqrt(3) + 1)`
⇒ x = `100 xx ((sqrt(3) + 1))/(3-1) = 50(sqrt(3) + 1) = 50 xx 2.732 = 136.6`
Thus , the distance of the point where he falls on the ground from the nearest observation point (C) is 136.6 m.
Height from which the parachutist fall
= h = `sqrt(3)"x" = 1.732 xx 136.6 = 236.59 ≈ 236.6` m.
APPEARS IN
RELATED QUESTIONS
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.
A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
The top of a ladder reaches a pcint on the wall 5 m above the ground. If the foot of the ladder makes an angle of 30° with the ground, find the length of the ladder.
A ladder rests against a tree on one side of a street. The foot of the ladder makes an angle of 50° with the ground. When the ladder is turned over to rest against another tree on the other side of the street it makes an angle of 40° with the ground. If the length of the ladder is 60m, find the width of the street.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
The horizontal distance between towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60m, find the height of the first tower.
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
