Advertisements
Advertisements
Question
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
Solution
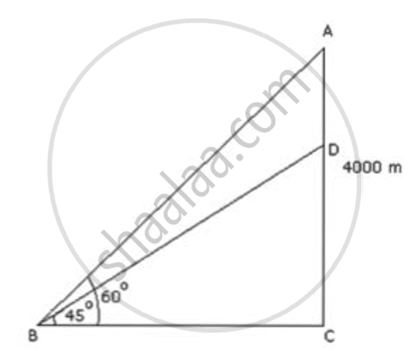
Let points A and D represent the position of the aeroplanes.
Aeroplane A is flying 4 km = 4000 m above the ground.
∠ACB = 60°, ∠DCB = 45°
In ΔABC,
`"AB"/"BC" = tan 60^circ`
⇒ `"BC" = 4000/sqrt(3)`
In ΔDCB,
`"DB"/"BC" = tan 45^circ`
⇒ DB = BC = `4000/sqrt(3)`
∴ AD = AB - BD
= `4000 - 4000/sqrt(3) = 4000(1 - 1/sqrt(3)) = 4000 xx (sqrt(3) - 1)/sqrt(3) = 4000 xx 0.732/1.732 = 1690.53`
= h = `sqrt(3)"x" = 1.732 xx 136.6 = 236.59 ≈ 236.6` m
APPEARS IN
RELATED QUESTIONS
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30° with the ground.
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate:
- the length of AB;
- the distance of AB from the centre C.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
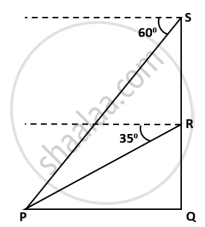
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.
An aeroplane is flying horizontally along a straight line at a height of 3000 m from the ground at a speed of 160 m/s. Find the time it would take for the angle of elevation of the plane as seen from a particular point on the ground to change from 60⁰ to 45⁰. Give your answer correct to the nearest second.
