Advertisements
Advertisements
Question
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
Solution
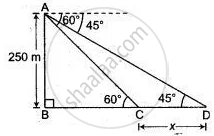
Let the width of the river CD be x,
In ΔABC,
tan 60° = `"AB"/"BC"`
√3 = `250/"BC"`
BC = `250/sqrt3 xx sqrt3/sqrt3`
BC = `(250/3)sqrt3` .....(i)
In Δ ABD,
tan 45° = `"AB"/"BD"`
⇒ AB = BD = 250 ....(ii)
∴ BD = BC + CD
∴ 250 = `(250/3) sqrt3 + x` ....(using (i) and (ii))
∴ x = 250 - `(250/3) xx 1.732`
∴ x = 250 - 83.33 x 1.732
∴ x = 250 - 144.33
∴ x = 105.67 m
∴ x = 106 m .....(to the nearest whole numbers)
Thus, width of the river is 106 m.
APPEARS IN
RELATED QUESTIONS
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68° with the ground. Find the height, upto which the ladder reaches.
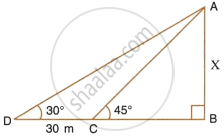
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
A boy is standing on the ground and flying a kite with 100m of sting at an elevation of 30°. Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
Two boats approaching a light house in mid sea from opposite directions observe the angle of elevation of the top of the light house as 30° and 45° respectively. If the distance between the two boats is 150m, find the height of the light house.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
A man on the top of vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower? (Give your answer correct to nearest seconds).
A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
