Advertisements
Advertisements
Question
A man on the top of vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower? (Give your answer correct to nearest seconds).
Solution
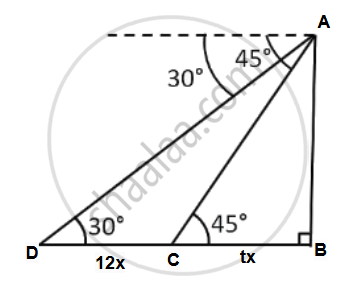
Here, ∠ACB = 30° and ∠ADB = 45°.
Let C denote the initial position of the car and D be its position after 12 minutes.
Let the speed of the car be x meter/minute, then
CD = 12x meters .....( ∵ Distance = speed x Time)
Let the car take t minutes to reach the tower from D.
Then, DB = tx meters
Now in the right-angled triangles ACB,
tan 30° = `"AB"/"BD"`
⇒ `1/sqrt3 = "AB"/("BC" + "CD")`
⇒ `1/sqrt3 = "AB"/(12x + tx)`
⇒ `"AB" = (12x + tx)/sqrt3` ....(1)
Also, in the right-angled triangle ADB,
tan 45° = `"AB"/"DB"`
⇒ 1 = `"AB"/"DB"`
⇒ AB = DB = tx ......(2)
From (1) and (2), we have
t = `12/(sqrt3 - 1) = 12(sqrt3 + 1)/2`
t = `6(sqrt3 + 1)`
t = 15.39
∴ Time = 16.39 minutes
Time = 16 minutes 23 seconds.
APPEARS IN
RELATED QUESTIONS
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
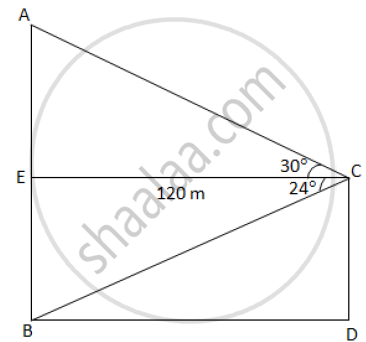
Find the height of the two towers. Give your answer correct to 3 significant figures
Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60° to 30°.
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° from two observing points 100 m apart to his right. Find the height from which he falls and the distance of the point where he falls on the ground from the nearest observation pcint.
