Advertisements
Advertisements
Question
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
Solution
Let AB be the tower and AB = x
Distance CD = 2y
In right ΔADB, we have
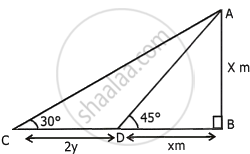
`tan theta = (AB)/(DB)`
`\implies tan 45^circ = x/(DB)`
`\implies 1 = x/(DB)`
`\implies` DB = x.
In right ΔACB, we have
`tan 30^circ = (AB)/(CB)`
`\implies 1/sqrt(3) = x/(CB)`
`\implies CB = sqrt(3)x`
`\implies x + 2y = sqrt(3)x`
∴ `sqrt(3)x - x = 2y`
`\implies x(sqrt(3) - 1) = 2y`
`x = (2y)/(sqrt(3) - 1)`
= `(2y(sqrt(3) + 1))/((sqrt(3) - 1)(sqrt(3) + 1))`
= `(2y(sqrt(3) + 1))/(3 - 1)`
= `(2y(sqrt(3) + 1))/2`
= `y(sqrt(3) + 1)`
∴ Required height of tower = `y(sqrt(3) + 1)`
APPEARS IN
RELATED QUESTIONS
A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
A ladder rests against a tree on one side of a street. The foot of the ladder makes an angle of 50° with the ground. When the ladder is turned over to rest against another tree on the other side of the street it makes an angle of 40° with the ground. If the length of the ladder is 60m, find the width of the street.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
An aeroplane at an altitude of 200 m observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river.
The angle of elevation of a tower from a point in line with its base is `45^circ` . On moving 20m towards the tower , the angle of elevation changes to `60^circ` . Find the height of the tower.
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.