Advertisements
Advertisements
Question
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
Solution
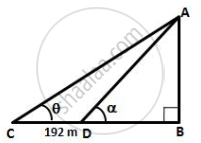
Let AB be the vertical tower and C and D be two point such that CD = 192 m. Let ∠ACB = θ and ∠ADB = α
Given, `tan theta = 5/12`
`=> (AB)/(BC) = 5/12`
`=> AB = 5/12 BC` ...(i)
Also, `tan alpha = 3/4`
`=> (AB)/(BD) = 3/4`
`=> ((5)/(12)BC)/(BD) = 3/4`
`=> (192 + BD)/(BD) = 3/4 xx 12/5`
`=>` BD = 240 m
∴ BC = (192 + 240) = 432 m
∴ By (i), `AB = 5/12 xx 432 = 180 m`
Hence, the height of the tower is 180 m.
APPEARS IN
RELATED QUESTIONS
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
Find AD.

The angles of depression and elevation of the top of a 12m high building from the top and the bottom of a tower are 60° and 30° respectively. Find the height of the tower, and its distance from the building.
Two boats approaching a light house in mid sea from opposite directions observe the angle of elevation of the top of the light house as 30° and 45° respectively. If the distance between the two boats is 150m, find the height of the light house.
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
An aeroplane is flying horizontally along a straight line at a height of 3000 m from the ground at a speed of 160 m/s. Find the time it would take for the angle of elevation of the plane as seen from a particular point on the ground to change from 60⁰ to 45⁰. Give your answer correct to the nearest second.
