Advertisements
Advertisements
Question
An aeroplane is flying horizontally along a straight line at a height of 3000 m from the ground at a speed of 160 m/s. Find the time it would take for the angle of elevation of the plane as seen from a particular point on the ground to change from 60⁰ to 45⁰. Give your answer correct to the nearest second.
Solution
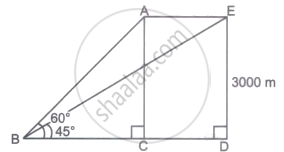
Given, AC = ED = 3,000 m
Speed = 160 m/s
In right ΔACB,
`tan 60^circ = "AC"/"BC"`
`=> sqrt3 = 3000/"BC"`
∴ BC = `3000/sqrt3`
`= 3000/sqrt3 xx sqrt3/sqrt3`
`= (3000 sqrt3)/3`
⇒ BC = `1000sqrt3` m
In right ΔEDB,
`tan 45^circ = "ED"/"BD"`
`=> 1 = 3000/"BD"`
⇒ BD = 3000 m
∴ AE = CD = BD - BC
∴ AE = 3000 - 1000`sqrt3`m
`= 1000 (3 - sqrt3)`
`= 1000 xx 1.268 ...(sqrt3 = 1.732)`
= 1268 m
∴ Time from A to E = `("Distance" ("AE"))/"Speed"`
`= 1268/160`
= 7.925 sec ≈ 8 sec
APPEARS IN
RELATED QUESTIONS
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°; find the uniform speed of the aeroplane in km per hour.
The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate:
- the length of AB;
- the distance of AB from the centre C.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
A 10 m high pole is kept vertical by a steel wire. The wire is inclined at an angle of 40° with the horizontal ground. If the wire runs from the top of the pole to the point on the ground where Its other end is fixed, find the lenqth of the wire.
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
An observer, 1.5m tall, is 28.5m away from a tower 30m high. Determine the angle of elevation of the top of the tower from his eye.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
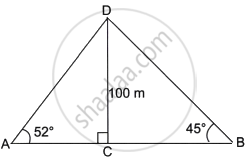
The angle of elevation of the top of a 100 m high tree from two points A and B on the opposite side of the tree are 52° and 45° respectively. Find the distance AB, to the nearest metre.