Advertisements
Advertisements
Question
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
Solution
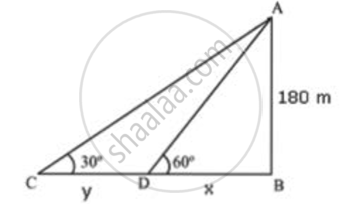
Let AB be the lighthouse.
Initial position of boat is C, which changes to D after 2 minutes.
In ΔADB
`"AB"/"DB" = tan60^circ`
`180/"x" = sqrt(3)`
`"x" = 180/sqrt(3)`
In ΔABC
`"AB"/"BC" = tan30^circ`
`180/("x + y") = 1/sqrt(3)`
`180sqrt(3) = "x + y"`
`180sqrt(3) = 180/sqrt(3) + "y"`
`"y" = 180(sqrt(3) - 1/sqrt(3)) = 180(2/sqrt(3)) = 360/sqrt(3)`
Time taken by car to travel DC distance `("i.e". 360/sqrt(3))` = 2 minutes = 120 seconds
Speed of the boat = `"Distance"/"Time" = (360/sqrt(3))/120 = 3/sqrt(3) = 3/sqrt(3) xx sqrt(3)/sqrt(3) = (3sqrt(3))/3 = sqrt(3) = 1.732`
Thus , the speed of the boat is 1.732 m/sec.
APPEARS IN
RELATED QUESTIONS
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
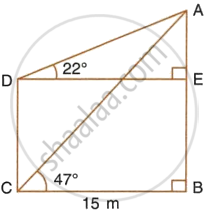
From the figure, given below, calculate the length of CD.
The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:
- the height of the tower,
- its horizontal distance from the points of observation.
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50 m away from the bank, he finds the angle of elevation to be 30°.
Calculate :
- the width of the river;
- the height of the tree.
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
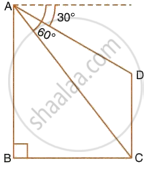
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
