Advertisements
Advertisements
Question
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
Solution
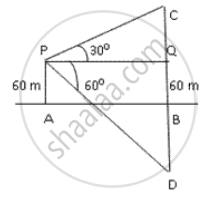
Let C be the cloud and D be its reflection . Let the height of the cloud is h metres .
BC = BD = h
BQ = AP = 60m
∴ CQ = h - 60 and DQ = h + 60
In ΔCQP,
`"PQ"/"CQ" = cot30^circ`
⇒ `"PQ"/("h" - 60) = sqrt(3)`
⇒ `"PQ" = sqrt(3)("h" - 60)"` ....(i)
In ΔDQP,
`"PQ"/"DQ" = cot60^circ`
⇒ `"PQ"/("h" + 60) = 1/sqrt(3)`
⇒ `"PQ" = 1/sqrt(3)("h" + 60)` ..(ii)
From (i) and (ii),
⇒ `sqrt(3)("h" - 60) = 1/sqrt(3)("h" + 60)`
⇒ 3h - 180 = h + 60
⇒ 2h = 240
⇒ h = 120
Thus , the height of the cloud is 120 m.
APPEARS IN
RELATED QUESTIONS
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50 m.
A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
From the top of a light house 96m high, the angles of depression of two ships in the river and at the same level as the base of the light house and on the same side of it, are α and β. If tan α = `1/4` and tan β = `1/7`, find the distance between the ships.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

From a lighthouse, the angles of depression of two ships on opposite sides of the lighthouse were observed to be 30° and 45°. If the height of the lighthouse is 90 metres and the line joining the two ships passes through the foot of the lighthouse, find the distance between the two ships, correct to two decimal places.
