Advertisements
Advertisements
Question
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
Solution
L.H.S. = tan2 A – sin2 A
= `sin^2A/cos^2A - sin^2A/1`
= `(sin^2A - sin^2A cos^2A)/(cos^2A)`
= `(sin^2A(1 - cos^2A))/cos^2A`
= `sin^2A/cos^2A (1 - cos^2A)`
= tan2 A sin2 A ...(∵ 1 – cos2 A = sin2 A)
= R.H.S.
APPEARS IN
RELATED QUESTIONS
Two climbers are at points A and B on a vertical cliff face. To an observer C, 40 m from the foot of the cliff, on the level ground, A is at an elevation of 48° and B of 57°. What is the distance between the climbers?
Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60° to 30°.
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
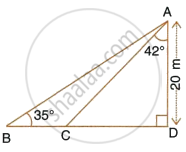
Calculate BC.
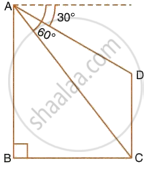
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
The horizontal distance between two trees of different heights is 100m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 150m, find the height of the first tree.
From a point 10 m above the ground , the angle of elevation of the top of a tower is α and the angle of depression is β . If tan α = `5/2` and tan β = `1/4` , calculate the height of the tower to the nearest metre .
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
If the angle of elevation of a cloud from a point h m above a lake is α, and the angle of depression of its reflection in the lake be β, prove that distance of the cloud from the point of observation is `("2h"secα)/(tanα - tanβ)`.
The angles of elevation of the top of a tower from two points A and B at a distance of a and b respectively from the base and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)`.
