Advertisements
Advertisements
Question
If the angle of elevation of a cloud from a point h m above a lake is α, and the angle of depression of its reflection in the lake be β, prove that distance of the cloud from the point of observation is `("2h"secα)/(tanα - tanβ)`.
Solution
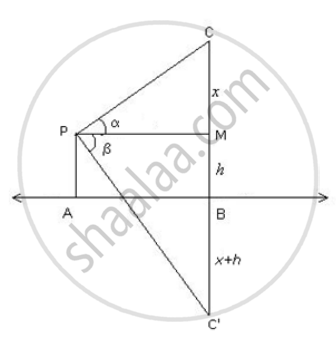
Let AB be the surface of the lake and let P be an point of observation such that AP = h meters . Let c be the position of the cloud and C' be its reflection in the lake . Then ∠CPM = α and ∠MPC = β. Let CM = x.
Then , CB = CM + MB = CM + PA = x + h
In ΔCPM,
tan α = `"CM"/"PM"`
⇒ `tan α = "x"/"AB"` [∵ PM = AB]
⇒ AB = x cotα ...(1)
In ΔPMC',
`tanβ = (C'M)/(PM)`
⇒ `tanβ = ("x" + "2h")/"AB"`
⇒ AB = (x + 2h)cotβ ....(2)
From (1) and (2),
x cotα = (x + 2h) cot β
⇒ `"x"(1/tanα - 1/tanβ) = "2h"/tanβ`
⇒ `"x"((tanβ - tanα) /(tanα tanβ)) = "2h"/tanβ`
⇒ x = `("2h"tanα)/(tanβ- tanα)`
Again, in Δ CPM,
`sin α = "CM"/"PC"` = `"x"/("PC")`
⇒ PC = `"x"/sin α`
⇒ `"PC" = ("2h"tanα)/(tanβ - tanα) xx 1/sin α`
⇒ `"PC" = ("2h"secα)/(tanβ - tanα)`
Hence , the distance of the cloud from the point of observation is `("2h"secα)/(tanβ - tanα)`.
APPEARS IN
RELATED QUESTIONS
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30° with the ground.
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
