Advertisements
Advertisements
Question
An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
Solution
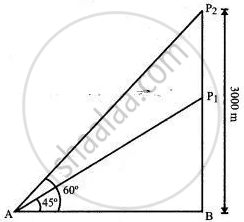
Let P1 and P2 denote the positions of the two planes. Then in right-angled ΔP1AB,
`(P_1B)/(AB) = tan 45° ⇒ P_1B = AB`
In right-angled ΔP2AB,
⇒ `(P_2B)/AB = tan 60° = sqrt3`
⇒ AB = `(P_2B)/sqrt3`
⇒ AB = `3000/sqrt3`
⇒ AB = 1000√3
∴ Vertical distance between the two planes is P1P2 = P2B - P1B
= 3000 - 1000√3
= 1000( 3 - √3) m
APPEARS IN
RELATED QUESTIONS
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate:
- the length of AB;
- the distance of AB from the centre C.
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
The angle of elevation of a tower from a point in line with its base is `45^circ` . On moving 20m towards the tower , the angle of elevation changes to `60^circ` . Find the height of the tower.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
