Advertisements
Advertisements
Question
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
Solution
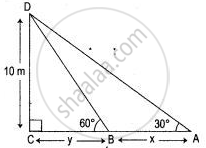
Let CD is building A and B are two given points using horizontally on the same side of building.
In Δ DBC,
tan 60° = `"DC"/"CB"`
√3 = `10/y` .....(1)
In Δ DCA,
tan 30° = `"DC"/"CA"`
`1/(√3) = 10/(x + y)` .....(2)
From (1), put y = `10/sqrt3` in (2), we get
`1/sqrt3 = 10/(x + 10/sqrt3)`
`1/sqrt3 = (10sqrt3)/(sqrt3x + 10)`
30 = √3x + 10
x = `20/sqrt3`
x = 11.55 m.
Hence, distance between two points A and B is 11.55 m.
APPEARS IN
RELATED QUESTIONS
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
From the top of a lighthouse, 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate:
- the length of AB;
- the distance of AB from the centre C.
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be α, and β. If the height of the light house is 'h' m and the line joining the ships passes through the foot of the light house, show that the distance between the ship is `("h"(tan α + tan β))/(tanα tanβ)`m.
