Advertisements
Advertisements
Question
A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
Solution
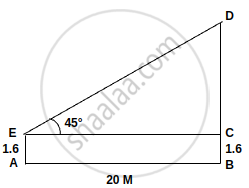
Let the height of the tower be h m.
i. Here, θ = 45°
∴ `tan 45^circ = (h - 1.6 )/20`
`=> 1 = (h - 1.6)/20`
∴ h = 21.6 m
So, height of the tower is 21.6 m
ii. Here θ = 60°
∴ `tan 60^circ = (h - 1.6)/20`
`=> sqrt(3) = (h - 1.6)/20`
∴ h = 20 × 1.732 + 1.6 = 36.24 m
So, height of the tower is 36.24 m.
APPEARS IN
RELATED QUESTIONS
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole is 60° and the angle of elevation of the top of the pole, as seen from the foot of the tower is 30°. Find:
- the height of the tower;
- the horizontal distance between the pole and the tower.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
A boy is standing on the ground and flying a kite with 100m of sting at an elevation of 30°. Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° from two observing points 100 m apart to his right. Find the height from which he falls and the distance of the point where he falls on the ground from the nearest observation pcint.
A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
