Advertisements
Advertisements
Question
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
Solution
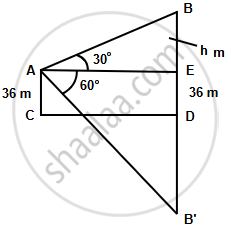
Let A be a point 36 m above the surface of the lake and B be the position of the bird. Let B' be the image if the brid in the water.
Here, AC = DE = 36 m, ∠BAE = 30° and ∠B’AE = 60°,
Let BE = h m,
Then, B'D = BD = 36 + h ...(∴ B’ is image of B about D)
∴ B’E = B’D + DE
= 36 + 36 + h
= 72 + h ...(i)
In ΔABE,
`(BE)/(AE) = tan 30^circ`
`=> AE = sqrt(3)h` ...(ii)
In ΔAB’E,
`(B^’E)/(AE) = tan 60^circ`
`=> (72 + h )/(AE) = sqrt(3)` ...[From (i)]
`=> 72 + h = (sqrt(3)h)sqrt(3)` ...[From (ii)]
`=>` 72 + h = 3h
∴ h = 36 m
Hence, the actual height of the bird above the surface of the lake = 36 + 36 = 72 m.
APPEARS IN
RELATED QUESTIONS
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28° and the angle of depression of the bottom of the pole is 13°. Calculate the height of the pole.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
From a point 10 m above the ground , the angle of elevation of the top of a tower is α and the angle of depression is β . If tan α = `5/2` and tan β = `1/4` , calculate the height of the tower to the nearest metre .
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.

