Advertisements
Advertisements
प्रश्न
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
उत्तर
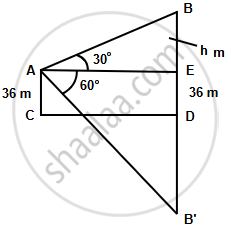
Let A be a point 36 m above the surface of the lake and B be the position of the bird. Let B' be the image if the brid in the water.
Here, AC = DE = 36 m, ∠BAE = 30° and ∠B’AE = 60°,
Let BE = h m,
Then, B'D = BD = 36 + h ...(∴ B’ is image of B about D)
∴ B’E = B’D + DE
= 36 + 36 + h
= 72 + h ...(i)
In ΔABE,
`(BE)/(AE) = tan 30^circ`
`=> AE = sqrt(3)h` ...(ii)
In ΔAB’E,
`(B^’E)/(AE) = tan 60^circ`
`=> (72 + h )/(AE) = sqrt(3)` ...[From (i)]
`=> 72 + h = (sqrt(3)h)sqrt(3)` ...[From (ii)]
`=>` 72 + h = 3h
∴ h = 36 m
Hence, the actual height of the bird above the surface of the lake = 36 + 36 = 72 m.
APPEARS IN
संबंधित प्रश्न
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
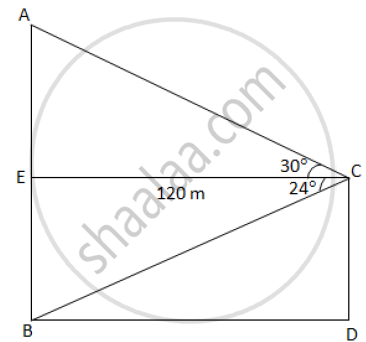
Find the height of the two towers. Give your answer correct to 3 significant figures
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
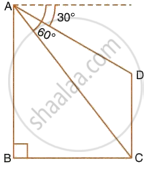
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
From the top of a light house 96m high, the angles of depression of two ships in the river and at the same level as the base of the light house and on the same side of it, are α and β. If tan α = `1/4` and tan β = `1/7`, find the distance between the ships.
From a point 10 m above the ground , the angle of elevation of the top of a tower is α and the angle of depression is β . If tan α = `5/2` and tan β = `1/4` , calculate the height of the tower to the nearest metre .
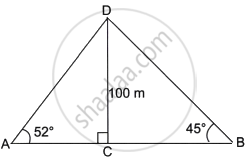
The angle of elevation of the top of a 100 m high tree from two points A and B on the opposite side of the tree are 52° and 45° respectively. Find the distance AB, to the nearest metre.