Advertisements
Advertisements
Question
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
Solution
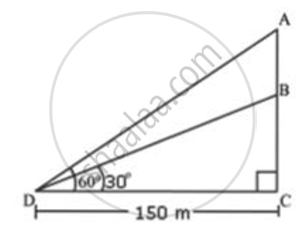
Let BC be the length of unfinished tower. Let the tower be raised upto point A so that the angle of elevation at point A is 60°. D is the point on ground from where elevation angles are measured.
In ΔBCD
`"BC"/"CD" = tan 30^circ`
`"BC"/"CD" = 1/sqrt(3)`
`"BC" = "CD"/sqrt(3)`
`"BC" = 150/sqrt(3)` ... (1)
In ΔACD
`("AB + BC")/("CD") = tan 60^circ`
⇒ `("AB + BC")/("CD") = sqrt(3)`
⇒ `("AB" + 150/sqrt(3))/150 = sqrt(3)` ....(Using (i))
⇒ `"AB" = 150sqrt(3) - 150/sqrt(3) = (150 xx 3 - 150)/sqrt(3)`
⇒ `"AB" = 300/sqrt(3) = 300/1.732 = 173.2` m
Thus , the required height is 300 m.
APPEARS IN
RELATED QUESTIONS
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
