Advertisements
Advertisements
Question
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

Solution
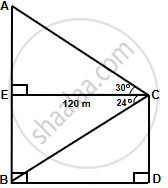
In ΔAEC,
`tan 30^circ = (AE)/(EC)`
`=> 1/sqrt(3) = (AE)/120`
`=> AE = 120/sqrt(3)`
= `120/sqrt(3) xx sqrt(3)/sqrt(3)`
= `(120sqrt(3))/3`
= `40sqrt(3)`
= 40 × 1.732
= 69.28 m
In ΔBEC,
`tan 24^circ = (EB)/(EC)`
`=> 0.4452 = (EB)/120`
`=>` EB = 53.424 m
Thus, height of first tower,
AB = AE + EB
= 69.28 + 53.424
= 122.704
= 123 m ...(Correct to 3 significant figures)
And height of second tower,
CD = EB
= 53.424 m
= 53.4 m ...(Correct to 3 significant figures)
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of an unfinished tower from a point at a distance of 80 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:
- the height of the tower,
- its horizontal distance from the points of observation.
Find AD.

The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
The horizontal distance between two trees of different heights is 100m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 150m, find the height of the first tree.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
