Advertisements
Advertisements
Question
A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
Solution
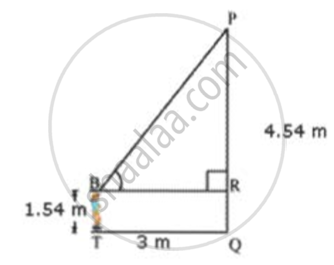
Let the position of the boy be at point T and P be the position of the sun.
BR = TQ = 3m
PQ = 4.54 m
BT = 1.54 m
.·.PR = 4.54 m - 1.54 m = 3 m
In ΔPRB
`"PR"/"BR" = tan θ`
`3/3 = tan θ`
tan θ = 1
We know that tan 45° = 1.
Thus, the angle of elevation is θ = 45°.
APPEARS IN
RELATED QUESTIONS
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
An observer, 1.5m tall, is 28.5m away from a tower 30m high. Determine the angle of elevation of the top of the tower from his eye.
A boy is standing on the ground and flying a kite with 100m of sting at an elevation of 30°. Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
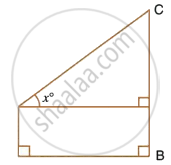
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
