Advertisements
Advertisements
Question
An observer, 1.5m tall, is 28.5m away from a tower 30m high. Determine the angle of elevation of the top of the tower from his eye.
Solution
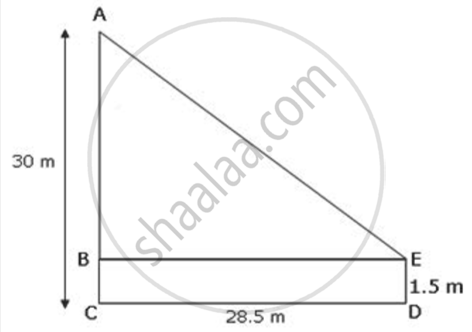
Here, ED is the height of the observer and AC is the tower.
BE = CD = 28. 5 m
AB = AC - BC = 30 m - 1.5 m = 28.5 m
In ΔABE,
`tan <"ABE" = "AB"/"BE"`
⇒ `tan <"ABE" = (28.5"m")/(28.5"m") = 1`
But, `tan 45^circ = 1`
`therefore <"ABE" = 45^circ`
Thus , the required angle of elevation is `45^circ`,
APPEARS IN
RELATED QUESTIONS
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
An aeroplane takes off at angle of `30^circ` with the ground . Find the height of the aeroplane above the ground when it has travelled 386m without changing direction .
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
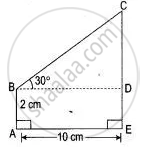
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
In figures, find the length CF.