Advertisements
Advertisements
Question
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
Solution
L.H.S. = sin4A – cos4A
= (sin2A)2 – (cos2A)2
= (sin2A + cos2A)(sin2A – cos2A)
= sin2A – cos2A
= sin2A – (1 – sin2A)
= 2sin2A – 1
= R.H.S.
APPEARS IN
RELATED QUESTIONS
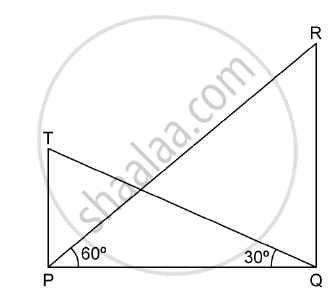
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre
A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
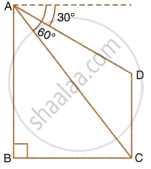
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
An aeroplane takes off at angle of `30^circ` with the ground . Find the height of the aeroplane above the ground when it has travelled 386m without changing direction .
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
The top of a ladder reaches a pcint on the wall 5 m above the ground. If the foot of the ladder makes an angle of 30° with the ground, find the length of the ladder.
A boy is standing on the ground and flying a kite with 100m of sting at an elevation of 30°. Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
Two boats approaching a light house in mid sea from opposite directions observe the angle of elevation of the top of the light house as 30° and 45° respectively. If the distance between the two boats is 150m, find the height of the light house.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
