Advertisements
Advertisements
Question
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
Solution
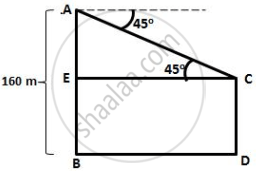
Let AB and CD be the two towers.
The height of the first tower is AB = 160 m
The horizontal distance between the two towers is BD = 75 m
And the angle of depression of the first tower as seen from the top of the second tower is ∠ACE = 45°
In ΔACE,
`(AE)/(EC) = tan 45^circ = 1`
`=>` AE = EC = BD = 75 m
∴ CD = EB
= AB – AE
= (160 – 75)
= 85 m
Hence, height of the other tower is 85 m.
APPEARS IN
RELATED QUESTIONS
Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60° to 30°.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
A 10 m high pole is kept vertical by a steel wire. The wire is inclined at an angle of 40° with the horizontal ground. If the wire runs from the top of the pole to the point on the ground where Its other end is fixed, find the lenqth of the wire.
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
