Advertisements
Advertisements
प्रश्न
A man on the top of vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower? (Give your answer correct to nearest seconds).
उत्तर
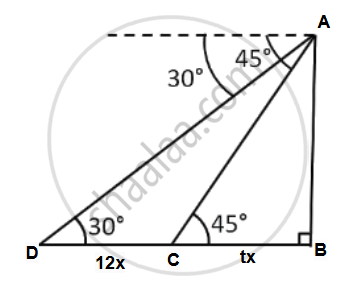
Here, ∠ACB = 30° and ∠ADB = 45°.
Let C denote the initial position of the car and D be its position after 12 minutes.
Let the speed of the car be x meter/minute, then
CD = 12x meters .....( ∵ Distance = speed x Time)
Let the car take t minutes to reach the tower from D.
Then, DB = tx meters
Now in the right-angled triangles ACB,
tan 30° = `"AB"/"BD"`
⇒ `1/sqrt3 = "AB"/("BC" + "CD")`
⇒ `1/sqrt3 = "AB"/(12x + tx)`
⇒ `"AB" = (12x + tx)/sqrt3` ....(1)
Also, in the right-angled triangle ADB,
tan 45° = `"AB"/"DB"`
⇒ 1 = `"AB"/"DB"`
⇒ AB = DB = tx ......(2)
From (1) and (2), we have
t = `12/(sqrt3 - 1) = 12(sqrt3 + 1)/2`
t = `6(sqrt3 + 1)`
t = 15.39
∴ Time = 16.39 minutes
Time = 16 minutes 23 seconds.
APPEARS IN
संबंधित प्रश्न
A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68° with the ground. Find the height, upto which the ladder reaches.
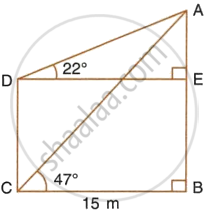
From the figure, given below, calculate the length of CD.
A man in a boat rowing away from a lighthouse 150 m high, takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 45°. Find the speed of the boat.
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
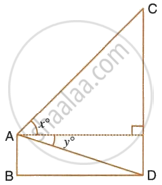
From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan `x^circ = 5/2` and the angle of depression of the foot D of the tower is y°, where tan `y^circ = 1/4`. Calculate the height CD of the tower in metres.
A man on the top of a tower observes a truck at an angle of depression ∝ where `∝ = 1/sqrt(5)` and sees that it is moving towards the base of the tower. Ten minutes later, the angle of depression of the truck is found to `β = sqrt(5)`. Assuming that the truck moves at a uniform speed, determine how much more ti me it will take to each the base of the tower?
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
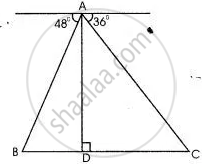
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
