Advertisements
Advertisements
प्रश्न
A man in a boat rowing away from a lighthouse 150 m high, takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 45°. Find the speed of the boat.
उत्तर
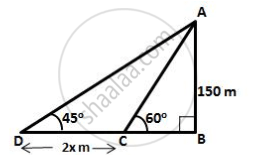
Let AB be the lighthouse and C and D be the two positions of the boat such that AB = 150 m, ∠ADB = 45° and ∠ACB = 60°.
Let speed of the boat be x metre per minute.
Therefore, CD = 2x m;
In ΔADB,
`(AB)/(DB) = tan 45^circ`
`=>` BD = 150 m
In ΔABC,
`(AB)/(BC) = tan 60^circ = sqrt(3)`
`=> 150/(BC)= sqrt(3)`
`=> BC = 150/ sqrt(3)`
= `150/1.732`
= 86.605 m
∴ CD = BD – BC
= 150 – 86.605
= 63.395 m
`=>` 2x = 63.395
`=> x = 63.395/2`
= 31.6975 m/min
= `31.6975/60` m/sec
= 0.53 m/sec
Hence, the speed of the boat is 0.53 m/sec
APPEARS IN
संबंधित प्रश्न
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if:
- the ships are on the same side of the light house,
- the ships are on the opposite sides of the light house.
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be 60°. Assuming that the boat sails at a uniform speed, determine:
- how much more time it will take to reach the shore?
- the speed of the boat in metre per second, if the height of the cliff is 500 m.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
