Advertisements
Advertisements
प्रश्न
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
उत्तर
Case 1: When the boats are on same side of the observation point.
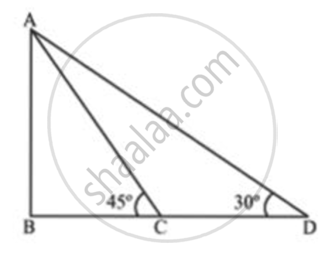
Let the position of the two ships be C and D. Let A be the point of observation.
AB = 500 m
In ΔBAC,
`tan45^circ = "AB"/"BC"`
⇒ `1 = 500/"BC"`
⇒ BC = 500 ....(1)
In ΔABD,
`tan30^circ = "AB"/"BD"`
⇒ `1/sqrt(3) = 500/"BD"`
⇒ `"BD" = 500sqrt(3)` ...(2)
From (1) and (2),
`"CD" = "BD" - "BC" = 500(sqrt(3) - 1) = 500 xx 0.732 = 366`
Thus, in this case, the distance between the boats is 366 m.
Case 2: When the boats are on different side of the observation point.
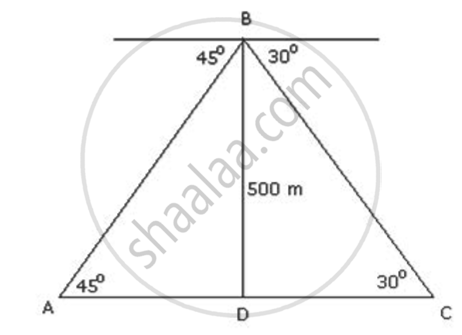
Let the position of the two ships be A and C. Let B be the point of observation.
In ΔBAD,
`tan45^circ = "BD"/"AD"`
⇒ `1 = 500/"AD"`
⇒ AD = 500 ....(1)
In ΔBDC,
`tan30^circ = "BD"/"DC"`
⇒ `1/sqrt(3) = 500/"DC"`
⇒ `"DC" = 500sqrt(3)` ....(2)
From (1) and (2),
`"AC" = "AD" + "DC" = 500 (1 + sqrt(3)) = 500 xx 2.732 = 1366`
Thus, in this case, the distance between the boats is 1366 m.
APPEARS IN
संबंधित प्रश्न
Find AD.

In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
An observer, 1.5m tall, is 28.5m away from a tower 30m high. Determine the angle of elevation of the top of the tower from his eye.
The horizontal distance between towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60m, find the height of the first tower.
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
