Advertisements
Advertisements
प्रश्न
The horizontal distance between towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60m, find the height of the first tower.
उत्तर
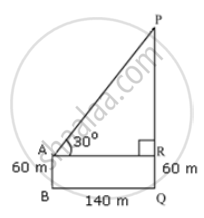
Let AB and PQ be the two towers.
BQ = AR = 140 m
AB = RQ = 60 m
Let PR = h
We need to find the height of the first tower, i.e. , PQ.
In ΔPRA,
`"PR"/"AR" = tan30^circ`
`"h"/140 = 1/sqrt(3)`
`"h" = 140/sqrt(3) = 80.83`
∴ PQ = PR + RQ = 80.83 m + 60 m = 140.83 m
Thus , the height of the first tower is 140.83 m.
APPEARS IN
संबंधित प्रश्न
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if:
- the ships are on the same side of the light house,
- the ships are on the opposite sides of the light house.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
The horizontal distance between two trees of different heights is 100m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 150m, find the height of the first tree.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
