Advertisements
Advertisements
प्रश्न
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
उत्तर
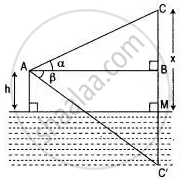
Let LM be the upper surface of the lake and A be a point such that AL = h.
Let C be the position of the cloud and C' be its reflection in the lake.
CM = MC' = x(let)
∠BAC = α and ∠BAC' = β
Now In ΔCBA,
tan α = `"CB"/"AB"`
tan α = `(x - h)/"AB"`
AB = `(x - h)/(tan α)` .....(i)
In ΔC'BA,
tan β = `"CB"/"AB"`
tan β = `(x + h)/"AB"`
AB = `(x + h)/tan β` .....(ii)
From (i) and (ii),
`(x - h)/(tan α) = (x + h)/tan β`
or `( x + h)/(x - h) = (tanβ)/(tan α)`
App. componendo and dividendo,
`( x + h + x - h )/(x + h - x + h) = (tanβ + tan α)/(tanβ - tan α)`
`( 2x)/(2h) = (tanβ + tan α)/(tanβ - tan α)`
`x = (h(tanβ + tan α))/(tanβ - tan α)`
∴ Height of the cloud is `x = (h(tanβ + tan α))/(tanβ - tan α)` ....Hence proved.
APPEARS IN
संबंधित प्रश्न
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
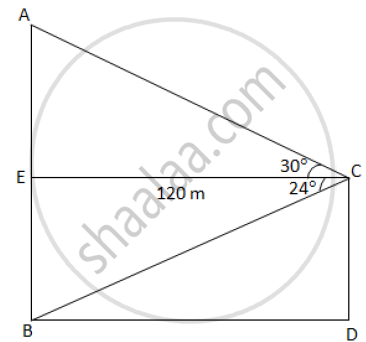
Find the height of the two towers. Give your answer correct to 3 significant figures
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be 60°. Assuming that the boat sails at a uniform speed, determine:
- how much more time it will take to reach the shore?
- the speed of the boat in metre per second, if the height of the cliff is 500 m.
A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
