Advertisements
Advertisements
प्रश्न
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
उत्तर
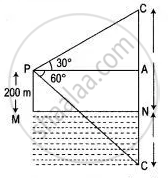
Let P be the point of observation and C, the position of cloud. CN ⊥ from C on the surface of the lake and C' be the reflection of the cloud in the lake so that
CN = NC' = x (say)
Then, PM = 200 m
∴ AN = MP = 200 m
CA = CN - AN = ( x - 200 ) m
C'A = NC' + AN = ( x + 200 ) m
Let, PA = y m
Then in right angled ΔPAC,
⇒ `(CA)/(PA) = tan 30°`
⇒ `(x - 200)/y = 1/sqrt3`
⇒ y = √3( x - 200) ....(i)
Also, in right angled ΔC'AP,
⇒ `(C'A)/(PA) = tan 60°`
⇒ `(x + 200)/y = sqrt3`
⇒ x + 200 = √3y
⇒ y = `( x + 200)/sqrt3` .....(ii)
From (i) and (ii),
⇒ `(x + 200)/sqrt3 = sqrt3(x - 200)`
⇒ x + 200 = 3( x - 200)
⇒ x + 200 = 3x - 600
⇒ 2x = 800
⇒ x = 400
Hence, the height of the cloud = 400 m.
APPEARS IN
संबंधित प्रश्न
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60° to 30°.
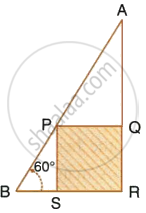
In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be α, and β. If the height of the light house is 'h' m and the line joining the ships passes through the foot of the light house, show that the distance between the ship is `("h"(tan α + tan β))/(tanα tanβ)`m.
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
