Advertisements
Advertisements
प्रश्न
The angles of elevation of the top of a tower from two points A and B at a distance of a and b respectively from the base and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)`.
उत्तर
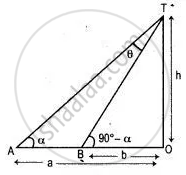
Let the height of the tower 'OT' = h.
Let O be the base of the tower.
Let A and B be two points on the same line through the base such that
OA = a, OB = b.
∵ The angles at A and B are complementary.
∴ ∠TAO = α
then ∠TBO = 90° - α
In right-angled ΔOAT,
tan α = `"OT"/"OA" = h/a` .....(i)
In right-angled ΔOBT,
tan(90° - α) = `"OT"/"OB" = h/b`
cot α = h/b` .....(ii)
Multiplying (i) and (ii), we have
tan α cot α = `h/a xx h/b = h^2/(ab)`
⇒ 1 = `h^2/(ab)`
⇒ h2 = ab
⇒ h = `sqrtab`
Hence, the height of the tower = `sqrtab`.
APPEARS IN
संबंधित प्रश्न
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°; find the uniform speed of the aeroplane in km per hour.
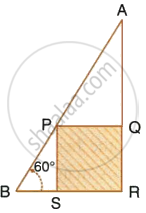
In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
An aeroplane takes off at angle of `30^circ` with the ground . Find the height of the aeroplane above the ground when it has travelled 386m without changing direction .
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
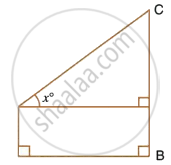
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
