Advertisements
Advertisements
Question
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
Solution
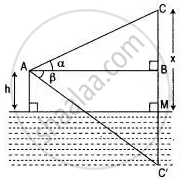
Let LM be the upper surface of the lake and A be a point such that AL = h.
Let C be the position of the cloud and C' be its reflection in the lake.
CM = MC' = x(let)
∠BAC = α and ∠BAC' = β
Now In ΔCBA,
tan α = `"CB"/"AB"`
tan α = `(x - h)/"AB"`
AB = `(x - h)/(tan α)` .....(i)
In ΔC'BA,
tan β = `"CB"/"AB"`
tan β = `(x + h)/"AB"`
AB = `(x + h)/tan β` .....(ii)
From (i) and (ii),
`(x - h)/(tan α) = (x + h)/tan β`
or `( x + h)/(x - h) = (tanβ)/(tan α)`
App. componendo and dividendo,
`( x + h + x - h )/(x + h - x + h) = (tanβ + tan α)/(tanβ - tan α)`
`( 2x)/(2h) = (tanβ + tan α)/(tanβ - tan α)`
`x = (h(tanβ + tan α))/(tanβ - tan α)`
∴ Height of the cloud is `x = (h(tanβ + tan α))/(tanβ - tan α)` ....Hence proved.
APPEARS IN
RELATED QUESTIONS
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60° to 30°.
From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if:
- the ships are on the same side of the light house,
- the ships are on the opposite sides of the light house.
The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate:
- the length of AB;
- the distance of AB from the centre C.
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
