Advertisements
Advertisements
प्रश्न
A parachutist is descending vertically and makes angles of elevation of 45° and 60° from two observing points 100 m apart to his right. Find the height from which he falls and the distance of the point where he falls on the ground from the nearest observation pcint.
उत्तर
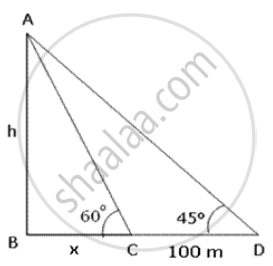
Let A be the position of the parachutist and C and D be the two observation points.
In ΔABC,
`tan 60^circ = "AB"/"BC"`
⇒ `sqrt(3) = "h"/"x"`
⇒ `"h" = sqrt(3"x")`
In ΔABD,
`tan 45^circ = "AB"/"BD"`
⇒ `1 = ("h"/("x" + 100))`
⇒ x + 100 = h
⇒ x + 100 = `sqrt(3)`x
⇒ `"x"(sqrt(3) - 1) = 100`
⇒ x = `100 xx 1/(sqrt(3) - 1) xx (sqrt(3) + 1)/(sqrt(3) + 1)`
⇒ x = `100 xx ((sqrt(3) + 1))/(3-1) = 50(sqrt(3) + 1) = 50 xx 2.732 = 136.6`
Thus , the distance of the point where he falls on the ground from the nearest observation point (C) is 136.6 m.
Height from which the parachutist fall
= h = `sqrt(3)"x" = 1.732 xx 136.6 = 236.59 ≈ 236.6` m.
APPEARS IN
संबंधित प्रश्न
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
Calculate BC.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
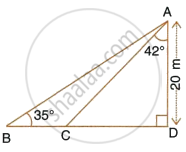
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

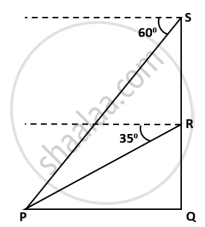
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.