Advertisements
Advertisements
प्रश्न
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
उत्तर
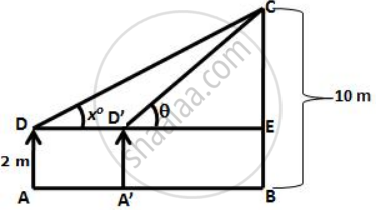
i. Let AD be the height of the man, AD = 2 m
∴ CE = (10 – 2) = 8 m
In ΔCED,
`(CE)/(DE) = tan x^circ = 2/5`
`=> 8/(DE) = 2/5 `
`=>` DE = 20 m
Here AB = DE
∴ AB = 20 m
ii. Let AD be the height of the man, AD = 2 m.
∴ CE = (10 – 2) = 8 m
Let A"D" be the new position of the man and θ be angle of elevation of the top of the tower.
So, D'E = 15 m
In ΔCED,
`tan theta = (CE)/(D^’E)`
= ` 8/15`
= 0.533
`=>` θ = 28°
संबंधित प्रश्न
Evaluate without using trigonometric tables.
`2((tan 35^@)/(cot 55^@))^2 + ((cot 55^@)/(tan 35^@)) - 3((sec 40^@)/(cosec 50^@))`
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
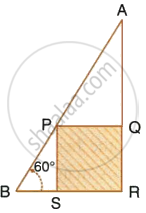
In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
An aeroplane takes off at angle of `30^circ` with the ground . Find the height of the aeroplane above the ground when it has travelled 386m without changing direction .
The angles of depression of two cars on a straight road as observed from the top of a 42m high building are 60° and 75° respectively. Find the distance between the cars if they are on opposite sides of the building.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
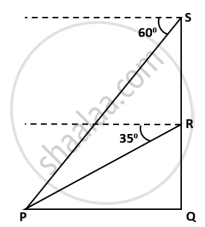
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.