Advertisements
Advertisements
प्रश्न
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
उत्तर
Let C be the position of the cloud, l be the surface of the lake and D be the reflection of the cloud.
Let CB = h, then OD = 25 + h
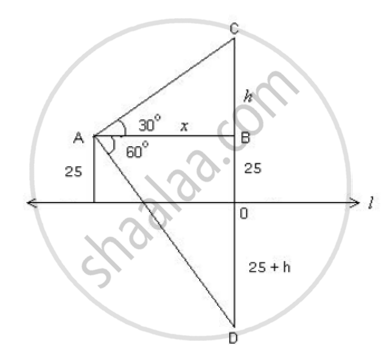
In ΔABC,
`tan 30^circ = "BC"/"AB"`
⇒ `1/sqrt(3) = "h"/"x"`
⇒ `sqrt(3)"h" = "x"` ...(1)
In ΔABD,
`tan 60^circ = "BD"/"AB" = (25 + 25 + "h")/"x"`
`sqrt(3)"x" = 50 + "h"` ...(2)
From (1) and (2),
`sqrt(3)(sqrt(3)"h") = 50 + "h"`
2h = 50
h = 25
Thus , the height of the cloud above the lake-level is OC = 50 m.
APPEARS IN
संबंधित प्रश्न
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to 30o and 60o respectively. Find:
1) The horizontal distance between AB and CD.
2) The height of the lamp post.
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50 m away from the bank, he finds the angle of elevation to be 30°.
Calculate :
- the width of the river;
- the height of the tree.
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
A 10 m high pole is kept vertical by a steel wire. The wire is inclined at an angle of 40° with the horizontal ground. If the wire runs from the top of the pole to the point on the ground where Its other end is fixed, find the lenqth of the wire.
From the top of a light house 96m high, the angles of depression of two ships in the river and at the same level as the base of the light house and on the same side of it, are α and β. If tan α = `1/4` and tan β = `1/7`, find the distance between the ships.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.

