Advertisements
Advertisements
Question
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.
Solution
Time is taken by bus to cover the total distance with speed x km/h = `240/x``
Time taken by bus to cover total distance with speed (x 10) km/h = `240/(x - 10)`
According to the given condition,
`240/(x-10) - 240/x = 2`
`=> 240 (1/(x - 10) - 1/x) = 2`
`=> 1/(x- 10) - 1/x = 1/120`
`=>(x - x + 10)/((x(x-10))) = 1/120`
`=> 10/(x^2 - 10x) = 1/120`
⇒ x2 - 10x = 1200
⇒ x2 - 10x - 1200 = 0
⇒ (x - 40)(x + 30) = 0
⇒ x- 40 = 0 or x = 30 = 0
⇒ x = 40 or x = -30
Since, the speed cannot be negative, the uniform speed is 40 km/h
APPEARS IN
RELATED QUESTIONS
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
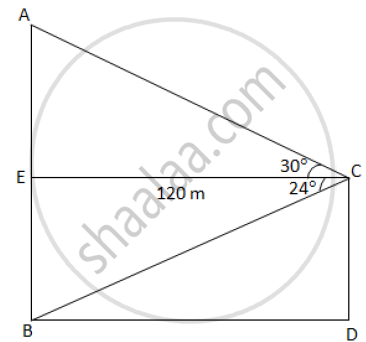
Find the height of the two towers. Give your answer correct to 3 significant figures
From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if:
- the ships are on the same side of the light house,
- the ships are on the opposite sides of the light house.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
Of the two trees are on either side of a river, one of them is 50m high. From the top of this tree the angles of depression of the top and the foot of the other tree are 30° and 60° respectively. Find the width of the river and the height of the other tree.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
A man on the top of vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower? (Give your answer correct to nearest seconds).
An aeroplane is flying horizontally along a straight line at a height of 3000 m from the ground at a speed of 160 m/s. Find the time it would take for the angle of elevation of the plane as seen from a particular point on the ground to change from 60⁰ to 45⁰. Give your answer correct to the nearest second.
