Advertisements
Advertisements
Question
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
Solution
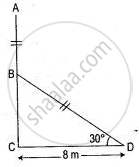
Let ABC be the pole. When broken at B by the wind, let it's top A strike the ground such that
∠ CAB = 30°
AC = 8 m
In ΔACB,
tan 30° = `"BC"/"AC"`
`1/sqrt3 = "BC"/8`
`BC = 8/sqrt3`
Again In ΔACB,
cos 30° = `"AC"/"AB"`
`sqrt3/2 = 8/"AB"`
AB = `16/sqrt3`
Height of the pole = AC = AB + BC
= `16/sqrt3 + 8/sqrt3`
= 8√3 m or 13.86 m.
APPEARS IN
RELATED QUESTIONS
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
The horizontal distance between towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60m, find the height of the first tower.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
