Advertisements
Advertisements
प्रश्न
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
उत्तर
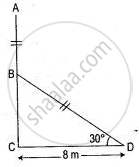
Let ABC be the pole. When broken at B by the wind, let it's top A strike the ground such that
∠ CAB = 30°
AC = 8 m
In ΔACB,
tan 30° = `"BC"/"AC"`
`1/sqrt3 = "BC"/8`
`BC = 8/sqrt3`
Again In ΔACB,
cos 30° = `"AC"/"AB"`
`sqrt3/2 = 8/"AB"`
AB = `16/sqrt3`
Height of the pole = AC = AB + BC
= `16/sqrt3 + 8/sqrt3`
= 8√3 m or 13.86 m.
APPEARS IN
संबंधित प्रश्न
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
A 10 m high pole is kept vertical by a steel wire. The wire is inclined at an angle of 40° with the horizontal ground. If the wire runs from the top of the pole to the point on the ground where Its other end is fixed, find the lenqth of the wire.
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
If the angle of elevation of a cloud from a point h m above a lake is α, and the angle of depression of its reflection in the lake be β, prove that distance of the cloud from the point of observation is `("2h"secα)/(tanα - tanβ)`.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

An aeroplane is flying horizontally along a straight line at a height of 3000 m from the ground at a speed of 160 m/s. Find the time it would take for the angle of elevation of the plane as seen from a particular point on the ground to change from 60⁰ to 45⁰. Give your answer correct to the nearest second.
