Advertisements
Advertisements
प्रश्न
The shadow of a vertical tower on a level ground increases by 10 m when the altitude of the sun changes from 45° to 30°. Find the height of the tower, correct to two decimal places.
उत्तर
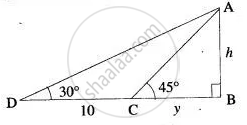
Let the height of tower be h meter and length of shawdow y meter initially.
In ΔABC,
tan 45° = `"AB"/"BC"`
1 = `h/y`
y = h ...(1)
In ΔABD,
tan 30° = `"AB"/"DB"`
`1/sqrt3 = h/(y + 10)`
y + 10 = h`sqrt3` ...(2)
Put y = h in equation (ii),
h + 10 = `hsqrt3`
`h(sqrt3 - 1) = 10`
h = `10(sqrt3 + 1)/((sqrt3 - 1)(sqrt3 + 1))`
h = `10/(3 - 1) (sqrt3 + 1)`
h = `10/2(sqrt3 + 1)`
h = 5(1.732 + 1)
h = 5 × 2.732
h = 13.66 meter
APPEARS IN
संबंधित प्रश्न
Evaluate without using trigonometric tables.
`2((tan 35^@)/(cot 55^@))^2 + ((cot 55^@)/(tan 35^@)) - 3((sec 40^@)/(cosec 50^@))`
A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:
- the height of the tower,
- its horizontal distance from the points of observation.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
An aeroplane, at an altitude of 250 m, observes the angles of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. If the boats are on the opposite sides of the aeroplane, find the width of the river. Write the answer correct to the nearest whole number.
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
A ladder rests against a tree on one side of a street. The foot of the ladder makes an angle of 50° with the ground. When the ladder is turned over to rest against another tree on the other side of the street it makes an angle of 40° with the ground. If the length of the ladder is 60m, find the width of the street.
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

